zkkKillua's Blog
0%

发表于 更新于 分类于

1. 顺序遍历

逐个判断，时间O(n)，空间O(1)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int findMagicIndex(vector<int>& nums) {
        int n = nums.size();
        int ans = -1;
        for (int i = 0; i < n; i++) {
            if (i == nums[i]) {
                ans = i;
                break;
            }
        }

        return ans;
    }
};

发表于 更新于 分类于

1. 数学

分析将一个数拆成以下部分：
拆1：没用
拆2：可以
拆3：可以
拆4：可以，跟2一样
拆5+：对半拆分后的乘积要比原来的值大
综上，尽可能拆出3，不要剩余1.
时间O(1)，空间O(1)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int integerBreak(int n) {
        if (n <= 3)
            return n - 1;

        int n3 = n / 3;
        int n2 = 0;
        n %= 3;
        if (n == 1) {
            n3--;
            n2 = 2;
        } else if (n == 2)
            n2 = 1;

        return pow(3, n3) * pow(2, n2);
    }
};

发表于 更新于 分类于

1. 辅助数组

bool类型的1~n的数组记录数据的出现情况，n为数据的个数。
时间O(n)，空间O(n)。

2. 原地重排

题目要求空间是O(1)的，单纯使用额外变量又没法记录得到最小值，同时又不能使用额外的空间，因此考虑原地重排。
数据和位置的对应关系如下： 

1
2
[3,4,-1,1]
 0,1, 2,3
阅读全文 »

发表于 更新于 分类于

1. 单调栈

使用一个辅助的单调递减栈，栈内存放数据的索引。
当当前元素大于栈顶元素时，弹出栈顶元素，并同时可以得到弹出的栈顶元素距离右侧第一个大于它的元素的位置。
当当前元素小于等于栈顶元素时，入栈。
时间O(n)，空间O(n)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& T) {
        stack<int> s;
        int n = T.size();
        vector<int> ans(n, 0);
        
        for (int i = 0; i < n; i++) {
            if (s.empty() || T[i] <= T[s.top()])
                s.push(i);
            else {
                int topIndex = s.top();
                while (!s.empty() && T[i] > T[topIndex]) {
                    s.pop();
                    ans[topIndex] = i - topIndex;
                    if (s.empty()) 
                        break;
                    topIndex = s.top();
                }
                s.push(i);
            }
        }

        return ans;
    }
};

发表于 更新于 分类于

1. 朴素

错误！！ 

1
2
3
4
5
6
输入:
"()(()"
输出
4
预期结果
2

题目要求的是子串，而不是任意匹配即可。
求从每一个’(‘的位置开始，最长的有效括号子串的长度。
时间O(n^2)，空间O(1)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int longestValidParentheses(string s) {
        int n = s.length();
        int ans = 0;

        for (int i = 0; i < n; i++) {
            if (s[i] == ')')
                continue;
            int temp = 0, llen = 1;
            for (int j = i + 1; j < n; j++) {
                if (s[j] == '(')
                    llen++;
                else {
                    if (llen > 0) {
                        llen--;
                        temp++;
                    } else
                        break;
                }
                ans = ans >= temp ? ans : temp;
            }
        }

        return ans * 2;     // 返回的是子串的长度
    }
};
阅读全文 »

发表于 更新于 分类于

1. 递归

时间O(n)，空间O(height)（递归栈） 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr)
            return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

2. 迭代

类似层次遍历，时间O(n)，空间O(n).

阅读全文 »

发表于 更新于 分类于

1. dfs+记忆化搜索

其实就是dp的思想。
dp[i][j]代表nums[i][j]开始，能够得到的最长递增路径的长度.
则dp[i][j]依赖于上下左右四个位置中值比当前值大的位置。

这样存在的问题是依赖位置的dp值不一定是已经求得的。

一种方法是先从大到小排序，按这个顺序求解。

另一种方法是递归求依赖但还未求解的位置的值。

阅读全文 »

发表于 更新于 分类于

1. 双指针遍历

遍历s和t，时间O(len(t))，空间O(1)。
如果短字符串s有无限多个，则可以预先处理t，得到每个位置开始下一个给定字符的最近位置，这样就可以直接跳转到下一个需要的位置了。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool isSubsequence(string s, string t) {
        int n1 = s.length(), n2 = t.length();
        if (n1 == 0)
            return true;
        int i1 = 0, i2 = 0;
        bool ans = false;
        while (i2 < n2) {
            if (s[i1] == t[i2])
                i1++;
            if (i1 >= n1) {
                ans = true;
                break;
            }
            i2++;
        }

        return ans;
    }
};

发表于 更新于 分类于

1. dp

设 dp[i]为 N = i时Alice的胜负情况，则 dp[i]取决于 i的 [1, i - 1]范围内的因数。

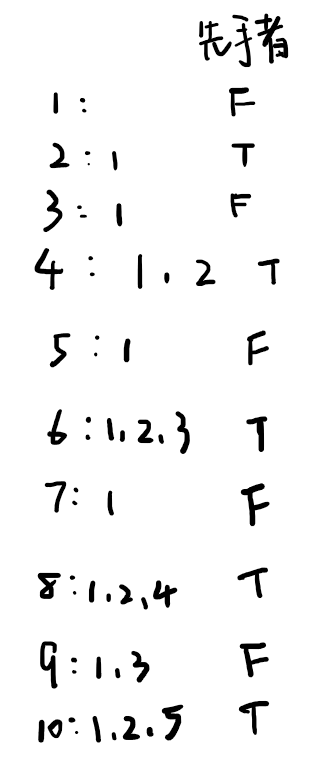
时间 O(n^2)，遍历 1~n是 O(n)，对每个数求因数又是 O(n)。空间复杂度 O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    bool divisorGame(int N) {
        vector<bool> dp(N + 1, false);
        for (int i = 2; i <= N; i++) {
            for (int j = 1; j < i; j++) {
                if (i % j == 0 && dp[i - j] == false) {
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[N];
    }
};
阅读全文 »

发表于 更新于 分类于

1. dp

因为不知道戳爆哪个气球得到的奖励最高，所以可以遍历i都戳戳试试。
当戳爆第i个气球时，得到nums[i - 1] * nums[i] * nums[i + 1]的奖励，
同时把气球分为左右两部分

假设首先戳爆i~j的气球k，则非常不好计算：
因为k被戳爆之后，左侧部分最后一个气球的戳爆依赖于右部分第一个气球，右侧部分第一个气球的戳爆依赖于左侧部分最后一个气球。
所以可以假设最后戳爆气球k，这样左右两部分就不会产生关联。

可以设dp[i][j]是戳爆nums[i] ~ nums[j]可得的最大收益。
dp[i][j] = max_k(dp[i][k - 1] + dp[k + 1][j] + nums[i - 1] * nums[k] * nums[j + 1])
时间O(n^3)，因为状态有O(n^2)种，每个状态的计算是O(n)。空间O(n^2)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    int maxCoins(vector<int>& nums) {
        int n = nums.size();
        if (n == 0)
            return 0;
        vector<vector<int>> dp(n, vector<int>(n, 0));
        
        for (int i = n - 1; i >= 0; i--) {
            for (int j = i; j < n; j++) {
                for (int k = i; k <= j; k++) {
                    dp[i][j] = max(dp[i][j], dpv(dp, i, k - 1) + dpv(dp, k + 1, j) + mult(nums, i, j, k));
                }
            }
        }

        return dp[0][n - 1];
    }
private:
    int dpv(const vector<vector<int>>& dp, const int& i, const int& j) {
        if (j < i)
            return 0;
        else
            return dp[i][j];
    }

    int mult(const vector<int>& nums, const int& i, const int& j, const int& k) {
        int a = i - 1 >= 0 ? nums[i - 1] : 1;
        int b = j + 1 < nums.size() ? nums[j + 1] : 1;
        return a * b * nums[k];
    }
};