zkkKillua's Blog
0%

发表于 更新于 分类于

1. 滑动窗口

因为只知道是字符，所以用hash表（unordered_map)来判重。
hash表中记录字符位置，当遇到重复时，跳过记录的该字符的位置到达下一个位置。
时间复杂度O(n)，空间复杂度O(字符数)（hash表占用） 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int len = s.length();
        if (len < 2)
            return len;

        unordered_map<char, int> loc;
        int ans = 0;
        int left = 0, right = 0;
        while (right < len) {
            if (loc.count(s[right]) == 1 && loc[s[right]] >= left) {
                ans = ans >= right - left ? ans : right - left;
                left = loc[s[right]] + 1;
            }
            loc[s[right]] = right;
            right++;
        }
        ans = ans >= right - left ? ans : right - left;

        return ans;
    }
};

发表于 更新于 分类于

1. 双指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode* ans = nullptr;
        ListNode* p = nullptr;
        while (l1 != nullptr || l2 != nullptr) {
            if (ans == nullptr) {
                if (l1 == nullptr || (l1 != nullptr && l2 != nullptr && l1->val > l2->val)) {
                    ans = new ListNode(l2->val);
                    l2 = l2->next;
                } else if (l2 == nullptr || (l1 != nullptr && l2 != nullptr && l1->val <= l2->val)) {
                    ans = new ListNode(l1->val);
                    l1 = l1->next;
                }
                p = ans;
                continue;
            }

            if (l1 == nullptr || (l1 != nullptr && l2 != nullptr && l1->val > l2->val)) {
                p->next = new ListNode(l2->val);
                p = p->next;
                l2 = l2->next;
            } else if (l2 == nullptr || (l1 != nullptr && l2 != nullptr && l1->val <= l2->val)) {
                p->next = new ListNode(l1->val);
                p = p->next;
                l1 = l1->next;
            }
        }

        return ans;
    }
};

发表于 更新于 分类于

1. 直接模拟，set检测是否重复

set：find()和count()对数级别复杂度，插入insert()在给定迭代器作为位置的情况下是O(1)，不给则是对数级别复杂度。
unordered_set：find()和count()平均是O(1)，最坏O(n)（hash函数太差了），插入insert()同查找。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    bool isHappy(int n) {
        unordered_set<int> unique;
        unique.insert(n);
        int copyn = n;
        while (n != 1) {
            n = 0;
            while (copyn != 0) {
                n += pow((copyn % 10), 2);
                copyn /= 10;
            }
            copyn = n;
            if (unique.count(n) == 1)
                return false;
            else
                unique.insert(n);
        }

        return true;
    }
};

2. 快慢指针

如果有结果，那么就好像是一条链一样。
如果没结果，不是快乐数，则代表有循环，也就可以转换成环形链表来做，快慢指针重合时代表不是快乐数。
这样就避免了set一直存数。
时间上跟unordered_set一样都是O(logn)，空间更优，是O(1)。

阅读全文 »

发表于 更新于 分类于

1. 二分

二分，然后根据左右大小关系判断是上升还是下降，选择不同部分继续二分就好了。
本来打算一次二分做的，不过发现当nums[mid] > target时，两侧部分都需要进行二分。
所以还是先二分找到分界点，然后再二分左侧和右侧吧，最多是3次二分。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
/**
 * // This is the MountainArray's API interface.
 * // You should not implement it, or speculate about its implementation
 * class MountainArray {
 *   public:
 *     int get(int index);
 *     int length();
 * };
 */

class Solution {
public:
    int findInMountainArray(int target, MountainArray &mountainArr) {
        int n = mountainArr.length();
        int left = 0, right = n - 1;
        int ans = -1;
        int topIndex = -1, topValue = 0;

        while (left <= right) {
            int mid = (left + right) / 2;
            int midv = mountainArr.get(mid);
            int midrv = mountainArr.get(mid + 1);
            if (midv < midrv) {
                left = mid + 1;
                topIndex = mid + 1;
                topValue = midrv;
            }
            else {
                int midlv = mountainArr.get(mid - 1);
                if (midv < midlv) {
                    right = mid - 1;
                    topIndex = mid - 1;
                    topValue = midlv;
                } else {
                    topIndex = mid;
                    topValue = midv;
                    break;
                }
            }
        }

        if (target > topValue)
            return -1;
        else if (target == topValue)
            return topIndex;

        left = 0;
        right = topIndex;
        while (left <= right) {
            int mid = (left + right) / 2;
            int midv = mountainArr.get(mid);
            if (midv == target) {
                ans = mid;
                break;
            } else if (midv < target) 
                left = mid + 1;
            else
                right = mid - 1;
        }
        if (ans != -1)
            return ans;
        
        left = topIndex + 1;
        right = n - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            int midv = mountainArr.get(mid);
            if (midv == target) {
                ans = mid;
                break;
            } else if (midv < target)
                right = mid - 1;
            else
                left = mid + 1;
        }

        return ans;
    }
};

发表于 更新于 分类于

1. 位运算

异或^：相同为0，不同为1.
假如只有一个不成对出现的数字，则基于这个性质，成对出现的数字异或起来得到全0，再异或上这个数字，结果就是这个数字，所以只需要全部异或起来就可以了。（妙啊

如果有两个不成对出现的数字a, b，则全部异或得到a^b，并不是想要的答案。
我们可以想到，如果把数据分为两组，1组有a和一部分成对的数据，2组有b和剩余部分成对的数据，则1组全部异或得到a，2组全部异或得到b。
现在的问题是如何分为两组。
a^b得到的结果中，有的位是0，有的位是1，而1的位说明a和b在该位上不相等。
所以可以取任意一个为1的位，将该位为1的数据分到1组，该位为0的数据分到2组。
这样1和2一定可以分开。
而由于成对出现的数据在同一位上一定是相同的，所以也可以被分到同一个组中，这样分组就完成了。

实际上也并不需要显式地分成两部分。
只要在循环的时候判断某一位是01，然后对应的异或到相应位置就可以了。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> singleNumbers(vector<int>& nums) {
        int n = nums.size();
        if (n == 2)
            return nums;
        
        int allXor = 0;
        for (int i = 0; i < n; i++)
            allXor ^= nums[i];
        
        int loc = 1;
        while ((loc & allXor) == 0)
            loc <<= 1;
        
        int a = 0, b = 0;
        for (int i = 0; i < n; i++) {
            if ((nums[i] & loc) == 0)
                a ^= nums[i];
            else
                b ^= nums[i];
        }

        return {a, b};
    }
};

发表于 更新于 分类于

1. 二分查找

通过左和中的大小关系判断是升序还是中间旋转了。
时间O(logn)，空间O(1)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int n = nums.size();
        if (n == 0)
            return -1;
        
        int ans = -1;
        int left = 0, right = n - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[left] > target) {
                if (nums[mid] >= nums[left])
                    left = mid + 1;
                else {
                    if (nums[mid] > target)
                        right = mid - 1;
                    else if (nums[mid] < target)
                        left = mid + 1;
                    else {
                        ans = mid;
                        break;
                    }
                }
            } else if (nums[left] < target) {
                if (nums[mid] >= nums[left]) {
                    if (nums[mid] > target)
                        right = mid - 1;
                    else if (nums[mid] < target)
                        left = mid + 1;
                    else {
                        ans = mid;
                        break;
                    }
                } else 
                    right = mid - 1;
            } else {
                ans = left;
                break;
            }
        }

        return ans;
    }
};

发表于 更新于 分类于

1. 两个有序链表合并的扩展

每次比较k个链表，这样每合并出一个节点，就需要O(k^2)的时间。所以此处可以优化一下，使用堆就可以以O(klogk)的时间得到最小值，花费最大O(k)空间。
为了获得堆顶弹出的元素来自的链表，所以还需要一起记录一下，可以用pair。
插入一次需要O(logk)的时间，一共nk个元素都需要进出堆，所以时间复杂度为O(nklogk)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        int n = lists.size();
        if (n == 0)
            return nullptr;

        // pair->first记录节点值，pair->second记录来自的链表的编号
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> heap;
        vector<ListNode*> nextLocs(n);
        for (int i = 0; i < n; i++) {       // 初始化
            if (lists[i] != nullptr) {
                heap.push(make_pair(lists[i]->val, i));
                nextLocs[i] = lists[i]->next;
            } else 
                nextLocs[i] = nullptr;
        }

        if (heap.empty())
            return nullptr;
        pair<int, int> temp = heap.top();
        heap.pop();
        ListNode* ans = new ListNode(temp.first);
        ListNode* p = ans;
        if (nextLocs[temp.second] != nullptr) {
            heap.push(make_pair(nextLocs[temp.second]->val, temp.second));
            nextLocs[temp.second] = nextLocs[temp.second]->next;
        }
        while (!heap.empty()) {
            temp = heap.top();
            heap.pop();
            p->next = new ListNode(temp.first);
            p = p->next;
            if (nextLocs[temp.second] != nullptr) {
                heap.push(make_pair(nextLocs[temp.second]->val, temp.second));
                nextLocs[temp.second] = nextLocs[temp.second]->next;
            }
        }

        return ans;
    }
};

发表于 更新于 分类于

1. 递归+回溯

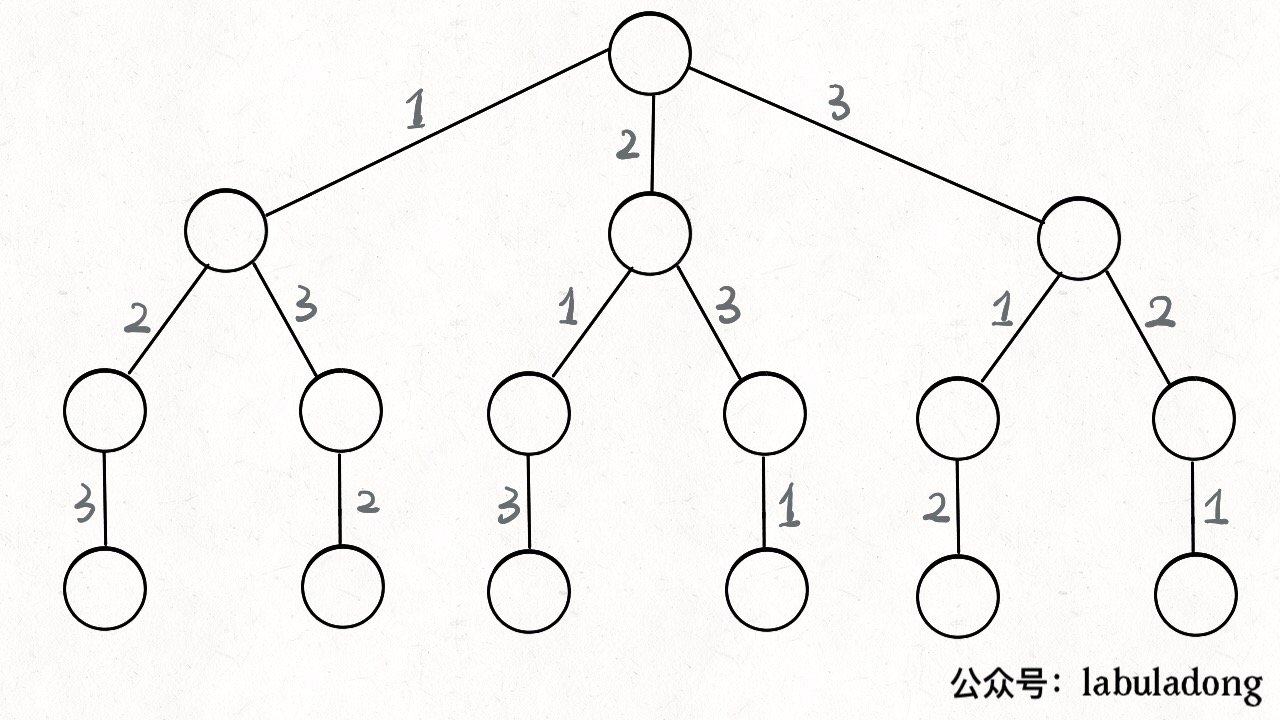
因为回溯是可以画出一棵回溯树的，所以光第一层调用dfs就要n次，而每次dfs还要层层深入，所以复杂度是很高的。
leetcode官方题解上分析出（组合数的加法），时间复杂度是 O(n*n!)，空间复杂度由于结果数组，所以是 O(n*n!)，如果不考虑结果数组的话，则是 O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        int n = nums.size();
      
        vector<vector<int>> ans;
        vector<int> cur(n);
        vector<bool> visited(n) {false};

        dfs(nums, cur, ans, visited, 0);
        return ans;
    }

    void dfs(vector<int>& nums, vector<int>& cur, vector<vector<int>>& ans, vector<bool>& visited, int count) {
        if (count == nums.size()) {
            ans.push_back(cur);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            if (!visited[i]) {
                cur[count] = nums[i];
                visited[i] = true;
                dfs(nums, cur, ans, visited, count + 1);
                visited[i] = false;
            }
        }
    }
};

发表于 更新于 分类于

1. 归并排序

归并排序的讲解见每日1题-912，归并排序的一个用途之一就是求解逆序对.
归并排序在每次合并的时候，如果是将右半部分的一个元素移入到合并后的数组中，则说明左侧数组中剩下部分的元素都大于右半部分的这个元素。
这样一下子就得到了好多逆序对。
只需要对原有的归并排序添加count即可。
时间复杂度O(nlogn)，空间复杂度O(n)，均同于归并排序。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
public:
    int reversePairs(vector<int>& nums) {
        int n = nums.size();
        if (n < 2)
            return 0;
        
        int ans = 0;
        vector<int> cpnums(nums);   // 不破坏原有数组nums
        vector<int> temp(n);        // 临时数组，避免内部频繁构造和析构
        mergeSort(cpnums, temp, 0, n - 1, ans);

        return ans;
    }

private:
    void mergeSort(vector<int>& nums, vector<int>& temp, int left, int right, int& count) {
        if (left >= right)
            return;
        
        int mid = (left + right) / 2;
        mergeSort(nums, temp, left, mid, count);       // 对左半部分排序
        mergeSort(nums, temp, mid + 1, right, count);  // 对右半部分排序

        // 合并有序的左右两部分

        if (nums[mid] <= nums[mid + 1])         // 已经有序
            return;

        int i = left, j = mid + 1;
        for (int k = left; k <= right; k++) {
            if (i > mid)
                temp[k] = nums[j++];
            else if (j > right)
                temp[k] = nums[i++];
            else {
                if (nums[i] <= nums[j])
                    temp[k] = nums[i++];
                else {
                    temp[k] = nums[j++];
                    count += mid - i + 1;
                }
            }
        }

        for (int k = left; k <= right; k++)
            nums[k] = temp[k];
    }
};

发表于 更新于 分类于

1. 数学方法

时间O(n)，空间O(1)，不过要是能继续把公式往下推的话，可能会有时间O(1)吧。 

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int waysToChange(int n) {
        int ans = 0;
        for (int i = 0; i <= n / 25; i++) {
            int temp = n - 25 * i;
            ans = (ans + (long long)(temp / 10 + 1) * (temp / 5 - temp / 10 + 1) % 1000000007) % 1000000007;
        }
        return ans;
    }
};

2. 完全背包的方案数

阅读全文 »