zkkKillua's Blog
0%

发表于 更新于 分类于

1. 快速幂

时间O(logn)，空间O(1)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    double myPow(double x, int n) {
        long long N = n;
        bool isNegative = x < 0 && N % 2 == 1;
        if (isNegative)
            x = -x;
        if (N < 0) {
            // n = -n;     // n == INT32_MIN时不能直接取负，会溢出
            N = -N;
            x = 1 / x;
        }
        double ans = 1;
        while (N > 0) {
            if (N & 1)
                ans *= x;
            x *= x;
            N >>= 1;
        }

        if (isNegative)
            ans = -ans;
        return ans;
    }
};

发表于 更新于 分类于

1. 二分

时间复杂度：O(logn)，空间复杂度O(1)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int mySqrt(int x) {
        if (x < 0)
            return -1;

        int left = 0, right = x;
        int ans = 0;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            long long midv = (long long)mid * mid;
            if (midv == x) {
                ans = mid;
                break;
            } else if (midv < x) {
                ans = mid;
                left = mid + 1;
            } else 
                right = mid - 1;
        }

        return ans;
    }
};

发表于 更新于 分类于

1. 动态规划

设 dp[i][j]代表以 matrix[i][j]为右下角的最大正方形的边长。
当 matrix[i][j] == 0时，dp[i][j] = 0.
当 matrix[i][j] == 1时，dp[i][j] = min(dp[i-1][j-1], dp[i][j-1], dp[i-1][j]) + 1.
如果越界，则上述min取0.

matrix[i][j] == 1的状态转移方程如上是因为：

  1. 假如 dp[i][j]根据 dp[i-1][j-1]来求，则需要判断i行j列的连续的1最多有多少，然后取 min(dp[i-1][j-1], i行的1, j列的1)再加上1就是 dp[i][j]。
  2. 假如 dp[i][j]根据 dp[i][j-1]来求，则需要判断j列的连续的1最多有多少，如果j列的小，则 dp[i][j] = j列 + 1，而如果j列的大，还需要判断 i-dp[i][j-1]行有没有足够的1使得可以形成 dp[i][j] = dp[i][j-1] + 1。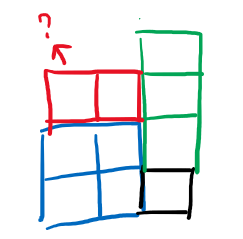
  3. 假如 dp[i][j]根据 dp[i-1][j]来求，则需要判断i行的连续的1最多有多少，如果i行的小，则 dp[i][j] = i行 + 1，而如果i行的大，还需要判断 j-dp[i][j-1]列有没有足够的1使得可以形成 dp[i][j] = dp[i-1][j] + 1。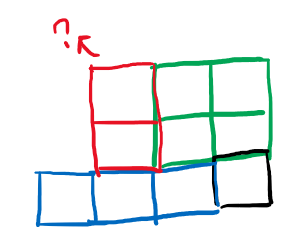

如果按照上面三种之一的求法，需要在遍历到每个点的时候，最多还要判断 O(min(m, n))次，因此时间复杂度是 O(mn*min(m, n))。
而我们可以发现，1需要的i行j列的连续的1的个数在 dp[i][j-1]和 dp[i-1][j]中分别有表示，2需要的j列的连续的1在 dp[i-1][j]中有所表示，需要的 i-dp[i][j-1]行的1的个数在 dp[i-1][j-1]和 dp[i][j-1]中有所表示。

阅读全文 »

发表于 更新于 分类于

1. 递归

两棵树相同，则所有的节点的值和位置相同。
可以通过递归比较根左右的想等情况。
时间复杂度：遍历所有节点O(n).
空间复杂度：递归栈最深是O(n). 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if (p == nullptr && q == nullptr)
            return true;
        if (p == nullptr || q == nullptr)
            return false;
        if (p->val != q->val)
            return false;
        return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

2. 迭代

相同的方法，不过用stack模拟递归栈来实现。
时间复杂度和空间复杂度与上述递归方法相同。

阅读全文 »

发表于 更新于 分类于

1. 动态规划（从前往后）

dp[i]代表从开始到第days[i]天(包括这一天)花费的钱。

如果求解dp[i]是遍历到i时再去看前1天、前7天和前30天花的钱+再买票的钱是没法计算的，因为前面的那些天已经买票了，即30天前的那一天可能已经花钱买了30天的票，如果再+票钱的话，就多余了。
所以就需要在dp[i]这天买票的时候，就将之后的在票范围内的dp[j]更新掉。

遍历到每一天days[i]，我们都假设这一天没有旅游，需要买票（加上上次旅游花的钱即dp[i-1]），并把买票之后可以访问到的dp[j]更新。
这样就可以得到每一个days[j]之前的天数花费一定的票费到达days[j]这一天。

如果是访问到days[i]这天发现已经通过之前的票旅游过了，那么这就是从开始到days[i]天花费的最少的钱。
而如果访问到days[i]这天，发现之前旅游买票还没有能长到这天的（即dp[i] == INT32_MAX时），就根据旅游到前一次花费的最少的钱dp[i-1]来更新dp[i]。

阅读全文 »

发表于 更新于 分类于

1. 中序遍历判断是否是递增序列

中序遍历：左根右
可以用递归实现，也可以用栈模拟递归栈来迭代实现，这里用迭代实现。
时间复杂度：遍历所有的节点，O(n)。
空间复杂度：递归栈，深度最大O(n)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        int pre = INT32_MIN;
        bool modified = false;
        stack<TreeNode*> st;

        while (root != nullptr || !st.empty()) {
            while (root != nullptr) {
                st.push(root);
                root = root->left;
            }
            root = st.top();
            st.pop();
            if (!modified) {
                pre = root->val;
                modified = true;
            } else {
                if (pre < root->val)
                    pre = root->val;
                else 
                    return false;
            }
            root = root->right;
        }

        return true;
    }
};

发表于 更新于 分类于

1. 朴素dp

dp[i]记录从开始到nums[i]节点需要的最少的跳数，则状态转移方程：
dp[i] = min(dp[j] + 1), if (j < i && j + nums[j] >= i)
时间O(n^2)，空间O(n)。
超时。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int jump(vector<int>& nums) {
        int n = nums.size();
        if (n < 2)
            return 0;
        
        int* dp = new int[n];
        for (int i = 1; i < n; i++)
            dp[i] = INT32_MAX;
        dp[0] = 0;
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (j + nums[j] >= i)
                    dp[i] = dp[i] <= dp[j] + 1 ? dp[i] : dp[j] + 1;
            }
        }

        int ans = dp[n - 1];
        delete []dp;
        return ans;
    }
};

2. 优化方法1的记录方式

可以在访问到i节点的时候，将其可以访问到的右侧的节点的dp[j]更新。
而由于定义的dp[i]数组一定是随着i的增加而增大的，所以之后的dp[j]只需要更新第一次即可。
由于只需要更新一次dp数组，所以时间复杂度是O(n)，空间复杂度也是O(n).

阅读全文 »

发表于 更新于 分类于

1. 朴素

bool reach[]记录是否可以到达。
遍历nums[i]，将其可以到达的位置置为true。时间复杂度是O(n)，因为就算修改reach[]是O(n)，但是还是可能会去访问后续的元素（即使没有修改），导致需要的时间很长。空间复杂度O(n)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n = nums.size();
        if (n <= 1)
            return true;
        bool *reach = new bool[n] {false};

        reach[0] = true;
        for (int i = 0; i < n; i++) {
            if (!reach[i])
                continue;
            for (int k = 1; k <= nums[i]; k++) {
                if (i + k >= n)
                    break;
                if (!reach[i + k])
                    reach[i + k] = true;
                if (i + k == n - 1) {       // 适当剪枝
                    delete []reach;
                    return true;
                }
            }
        }

        bool ans = reach[n - 1];
        delete []reach;
        return ans;
    }
};

2. 记录右侧最远距离

考虑题目要求，由于可走的长度是>=0的，因此可以直接记录最远的距离，而最远距离左侧的距离一定可达。
当当前距离超过最远距离时，意味着当前距离无法到达。
时间复杂度O(n)，空间复杂度O(1)。

阅读全文 »

发表于 更新于 分类于 
1
2
3
4
5
6
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        
    }
};

1. 滑动窗口

当窗口内的值为正时，右边界一直向右移动（因为左侧总是可以作为正数部分）
当窗口内的值为负时，左边界跳过右边界（因为左侧已经是负数了）
时间O(n)，空间O(1)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        if (n == 0)
            return 0;

        int loc = 0, ans = nums[0], cur = 0;
        while (loc < n) {
            if (cur >= 0) {
                cur += nums[loc++];
                ans = ans >= cur ? ans : cur;
            }
            else
                cur = 0;
        }

        return ans;
    }
};

2. 分治

阅读全文 »