zkkKillua's Blog
0%

221.最大正方形

发表于 更新于 分类于

1. 动态规划

设 dp[i][j]代表以 matrix[i][j]为右下角的最大正方形的边长。
当 matrix[i][j] == 0时，dp[i][j] = 0.
当 matrix[i][j] == 1时，dp[i][j] = min(dp[i-1][j-1], dp[i][j-1], dp[i-1][j]) + 1.
如果越界，则上述min取0.

matrix[i][j] == 1的状态转移方程如上是因为：

  1. 假如 dp[i][j]根据 dp[i-1][j-1]来求，则需要判断i行j列的连续的1最多有多少，然后取 min(dp[i-1][j-1], i行的1, j列的1)再加上1就是 dp[i][j]。
  2. 假如 dp[i][j]根据 dp[i][j-1]来求，则需要判断j列的连续的1最多有多少，如果j列的小，则 dp[i][j] = j列 + 1，而如果j列的大，还需要判断 i-dp[i][j-1]行有没有足够的1使得可以形成 dp[i][j] = dp[i][j-1] + 1。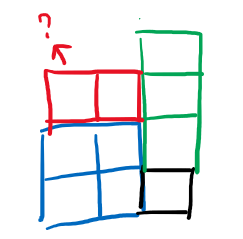
  3. 假如 dp[i][j]根据 dp[i-1][j]来求，则需要判断i行的连续的1最多有多少，如果i行的小，则 dp[i][j] = i行 + 1，而如果i行的大，还需要判断 j-dp[i][j-1]列有没有足够的1使得可以形成 dp[i][j] = dp[i-1][j] + 1。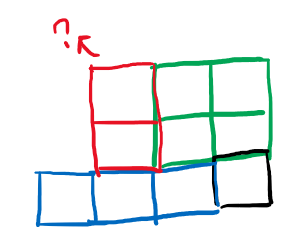

如果按照上面三种之一的求法，需要在遍历到每个点的时候，最多还要判断 O(min(m, n))次，因此时间复杂度是 O(mn*min(m, n))。
而我们可以发现，1需要的i行j列的连续的1的个数在 dp[i][j-1]和 dp[i-1][j]中分别有表示，2需要的j列的连续的1在 dp[i-1][j]中有所表示，需要的 i-dp[i][j-1]行的1的个数在 dp[i-1][j-1]和 dp[i][j-1]中有所表示。

所以我们发现，可以取 min(dp[i-1][j-1], dp[i][j-1], dp[i-1][j]) + 1作为 dp[i][j]，因为三者中最小的正方形要形成+1大的正方形需要的部分是另外两个较大的正方形可以提供的。

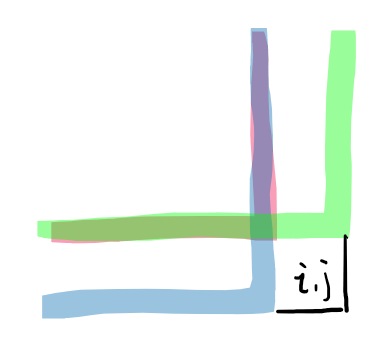
由上述状态转移方程可以得到时间复杂度 O(mn)，空间复杂度 O(mn)。
不过该空间复杂度可以优化，因为 dp[i][j]的求解仅依赖于左上方三个部分的值，所以可以将 O(mn)的数组优化为 O(n)的数组，只保留一行，空间复杂度就变成了 O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int m = matrix.size();
        if (m == 0)
            return 0;
        int n = matrix[0].size();

        vector<int> dp(n, 0);
        int mi[3] = {-1, 0, -1};
        int mj[3] = {-1, -1, 0};
        int ans = 0;

        for (int i = 0; i < m; i++) {
            int upperLeft = INT32_MAX;
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '0') {
                    upperLeft = dp[j];
                    dp[j] = 0;
                    continue;
                }

                int limit = INT32_MAX;
                for (int k = 0; k < 3; k++) {
                    int curi = i + mi[k], curj = j + mj[k];
                    if (curi >= 0 && curi < m && curj >= 0 && curj < n) {
                        if (mi[k] == -1 && mj[k] == -1)
                            limit = min(limit, upperLeft);
                        else 
                            limit = min(limit, dp[curj]);
                    } else {
                        limit = 0;
                        break;
                    }
                }
                if (limit == INT32_MAX)
                    limit = 0;
              
                upperLeft = dp[j];
                dp[j] = limit + 1;
                ans = max(ans, dp[j]);
            }
        }

        return ans * ans;
    }
};