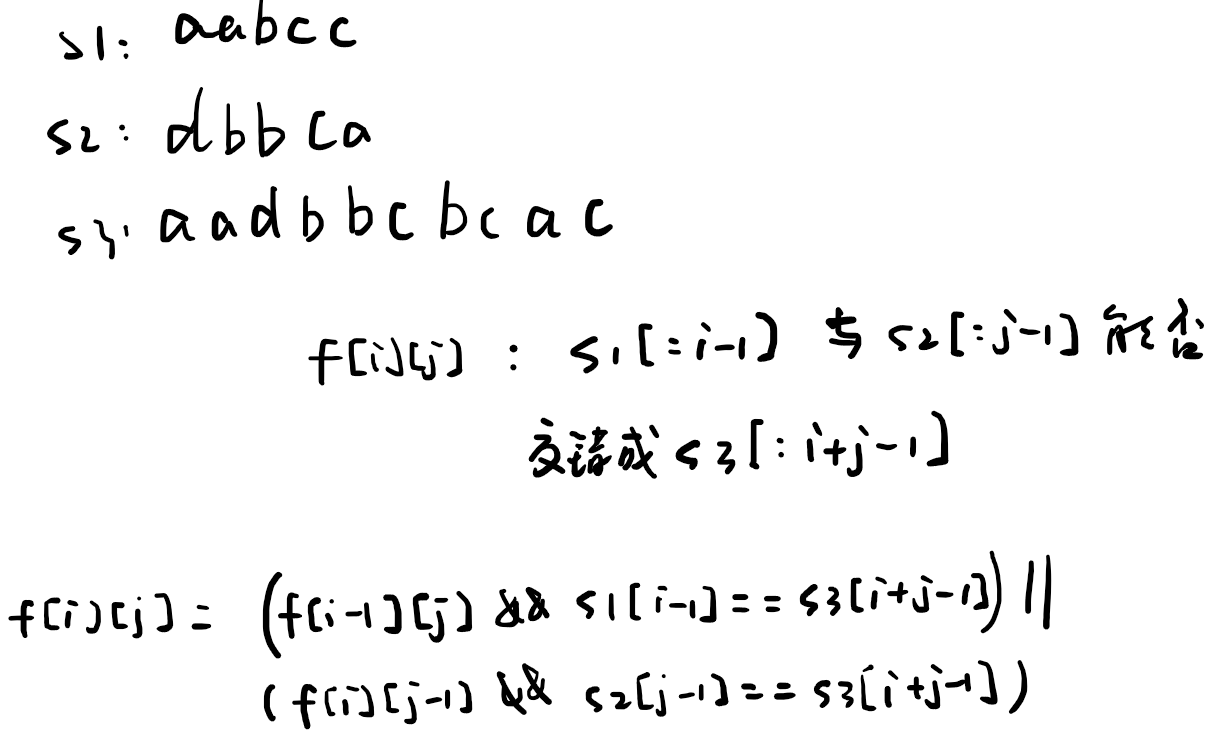1. 递归
第一反应是双指针,s3判断一个,对应的s1或者s2向后移一位。
但问题在于,当s1和s2的当前位相同时,无法确定s1/s2向后移位。
如果加上回溯,则跟递归类似。
复杂度指数级。
可以通过记忆化降低复杂度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
bool isInterleave(string s1, string s2, string s3) {
int m = s1.length(), n = s2.length();
if (m + n != s3.length())
return false;
if (m == 0 && n == 0)
return true;
else if (m == 0) {
if (s2[0] == s3[0])
return isInterleave(s1, s2.substr(1), s3.substr(1));
else
return false;
} else if (n == 0) {
if (s1[0] == s3[0])
return isInterleave(s1.substr(1), s2, s3.substr(1));
else
return false;
} else {
if (s1[0] == s3[0] && s2[0] != s3[0])
return isInterleave(s1.substr(1), s2, s3.substr(1));
else if (s1[0] != s3[0] && s2[0] == s3[0])
return isInterleave(s1, s2.substr(1), s3.substr(1));
else if (s1[0] == s3[0] && s2[0] == s3[0])
return isInterleave(s1.substr(1), s2, s3.substr(1)) || isInterleave(s1, s2.substr(1), s3.substr(1));
else
return false;
}
}
};
|
2. 动态规划
f[i][j]代表s1的前i个字符和s2的前j个字符是否符合s3的前i+j个字符。
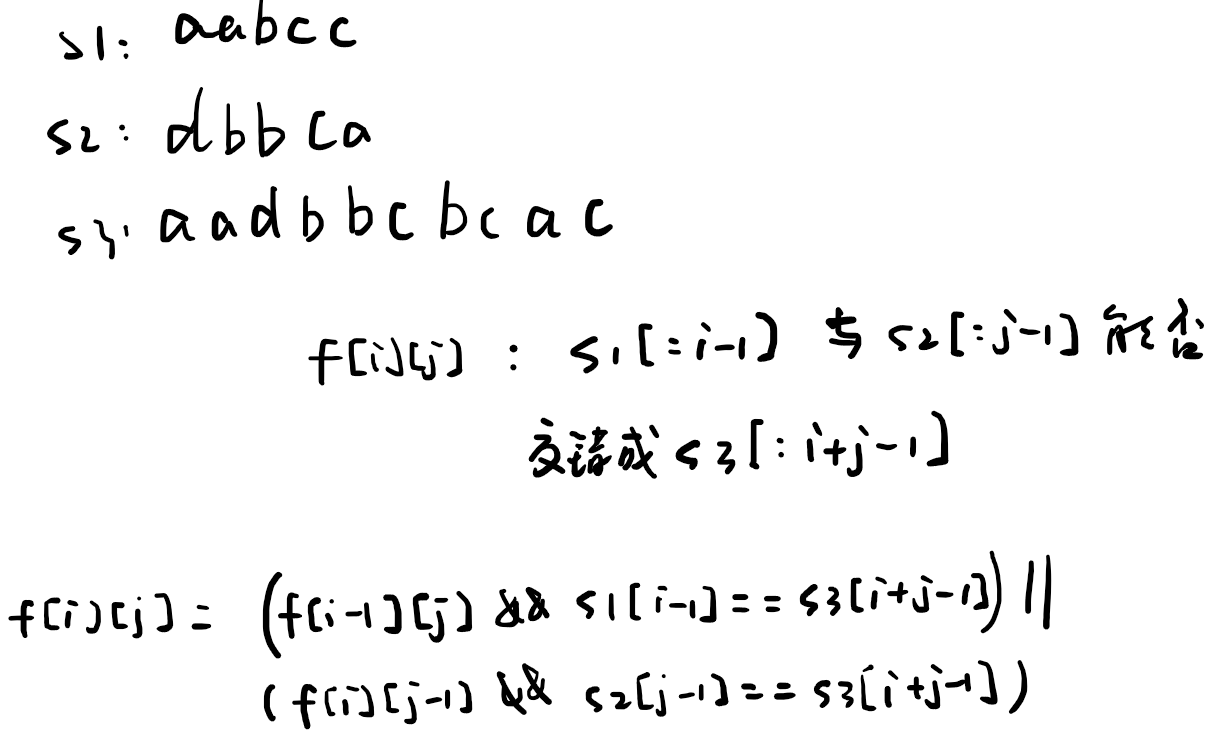
时间复杂度:O(mn)
空间复杂度:O(mn),但是因为更新只需要上一行,所以可以优化到 O(n)的空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public:
bool isInterleave(string s1, string s2, string s3) {
int m = s1.length(), n = s2.length();
if (m + n != s3.length())
return false;
vector<bool> dp(n + 1, false);
dp[0] = true;
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i > 0)
dp[j] = dp[j] && s1[i - 1] == s3[i + j - 1];
if (j > 0)
dp[j] = dp[j] || (dp[j - 1] && s2[j - 1] == s3[i + j - 1]);
}
}
return dp[n];
}
};
|