1025.除数博弈

1. dp

设 dp[i]为 N = i时Alice的胜负情况，则 dp[i]取决于 i的 [1, i - 1]范围内的因数。

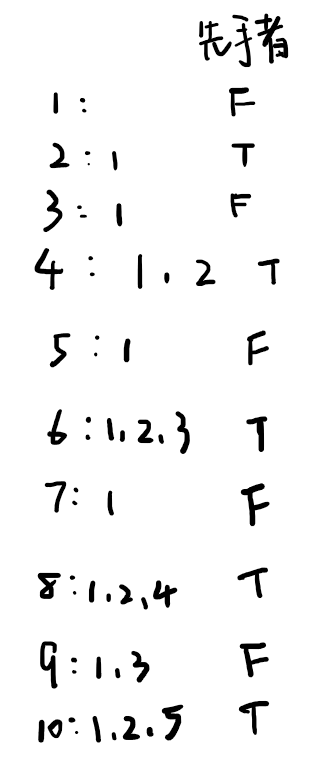
时间 O(n^2)，遍历 1~n是 O(n)，对每个数求因数又是 O(n)。空间复杂度 O(n)。

class Solution {
public:
    bool divisorGame(int N) {
        vector<bool> dp(N + 1, false);
        for (int i = 2; i <= N; i++) {
            for (int j = 1; j < i; j++) {
                if (i % j == 0 && dp[i - j] == false) {
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[N];
    }
};

2. 博弈数学

初始时只有 dp[1] = false和 dp[2] = true.
考虑对于之后的奇数节点，由于奇数的因数必为奇数，所以 dp[奇数]必转移到 dp[偶数].
而偶数的因数必有一个1，所以可以转移到前一个奇数，而奇数目前(dp[1])是必败的，所以偶数选1使对方必败，自己则必胜。
因此 dp[偶数]是必胜的，dp[奇数]被迫转移到偶数之后也必败。
所以只需要判断奇偶性即可，时间空间复杂度均为 O(1).

class Solution {
public:
    bool divisorGame(int N) {
        return N % 2 == 0 ? true : false;
    }
};